.ipynb .pdf

Binder

Contents

Решение нелинейных уравнений

Подмодуль scipy.optimize также содержит в себе методы для поиска корней нелинейных уравнений и их систем.

Поиск корня скалярной функции одного аргумента

Функция scipy.optimize.root_scalar позволяет искать корни функции \(f: \mathbb{R} \to \mathbb{R}\):

\[ f(x) = 0. \]

Функция root_scalar предоставляет доступ к разным методам поиска корней, таким как newton, bisect, secant и многим другим. Какие-то из этих методов ищут корень внутри отрезка bracket, а другие ищут корень, начиная с какого-то начального приближения x0.

import numpy as np
from scipy import optimize
from matplotlib import pyplot as plt


def f(x):
    return x**3 - 1

def fprime(x):
    return 3 * x**2


sol = optimize.root_scalar(f, bracket=[-10, 10], method="bisect")
print(sol)


x = np.linspace(-3, 3, 100)
plt.plot(x, f(x))
plt.scatter(sol.root, f(sol.root), color="r")
plt.xticks([1])
plt.yticks([0])
plt.xlabel("x")
plt.ylabel("y")
plt.legend(["f(x)", "Корень"])
plt.grid()

      converged: True
           flag: 'converged'
 function_calls: 46
     iterations: 44
           root: 1.0000000000002274

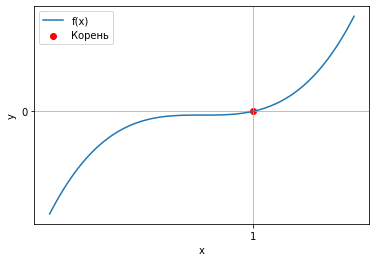
Метод бисекции сошелся за 44 итерации. Проверим метод Ньютона.

sol = optimize.root_scalar(f, fprime=fprime, x0=10, method="newton")
print(sol)

      converged: True
           flag: 'converged'
 function_calls: 22
     iterations: 11
           root: 1.0

Метод Ньютона сошелся за 11 итераций.

Решение системы нелинейных уравнений.

Функция \(F\) предназначена для поиска корней уравнений вида

\[ F(x) = 0, \]

где \(x\) и \(F(x)\) многомерны, т.е. таких систем

\[\begin{split} \begin{cases} f_1(x_1, ..., x_n) = 0 \\ \cdots \\ f_n(x_1, ..., x_n) = 0 \end{cases}. \end{split}\]

Рассмотрим поиск корня на примере функции

\[\begin{split} \begin{cases} x_1 + \frac{(x_1 - x_2)^3}{2} = 1 \\ \frac{(x_2 - x_1)^3}{2} + x_2 = 1 \end{cases}. \end{split}\]

Матрица Якоби этого уравнения имеет вид

\[\begin{split} \begin{pmatrix} 1 + \frac{3}{2}(x_2 - x_1)^2 & \frac{3}{2}(x_2 - x_1)^2 \\ \frac{3}{2}(x_2 - x_1)^2 & 1 + \frac{3}{2}(x_2 - x_1)^2 \end{pmatrix}, \end{split}\]

а единственный действительный корень которой

\[\begin{split} \begin{cases} x_1 = 1 \\ x_2 = 1 \end{cases}. \end{split}\]

import numpy as np
from scipy import optimize
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def f(x):
    x = np.array(x)
    return np.array([
        x[0]  + 0.5 * (x[0] - x[1])**3 - 1.0,
        0.5 * (x[1] - x[0])**3 + x[1] - 1.0
        ])


def jac(x):
    return np.array([[1 + 1.5 * (x[0] - x[1])**2,
                      -1.5 * (x[0] - x[1])**2],
                     [-1.5 * (x[1] - x[0])**2,
                      1 + 1.5 * (x[1] - x[0])**2]])


root = optimize.root(f, x0 = [0, 0])  
print(root)  

    fjac: array([[-1.00000000e+00, -1.09073861e-12],
       [ 1.09073861e-12, -1.00000000e+00]])
     fun: array([0., 0.])
 message: 'The solution converged.'
    nfev: 5
     qtf: array([-2.18114415e-12, -2.18114415e-12])
       r: array([-1.00000000e+00, -2.18119967e-12, -1.00000000e+00])
  status: 1
 success: True
       x: array([1., 1.])

root = optimize.root(f, jac=jac, x0 = [0, 0], method="hybr")  
print(root)  

    fjac: array([[-1.,  0.],
       [ 0., -1.]])
     fun: array([0., 0.])
 message: 'The solution converged.'
    nfev: 2
    njev: 1
     qtf: array([1., 1.])
       r: array([-1., -0., -1.])
  status: 1
 success: True
       x: array([1., 1.])

previous

Оптимизация

next

Пример