.ipynb .pdf

Binder

Contents

Интерполяция функций, аппроксимация функций

Интерполяция

Подмодуль scipy.interpolate содержит в себе методы для интерполяции.

Коротко про интерполяцию можно почитать в википедии. Более подробное изложение можно найти в [1].

Задача интерполирования состоит в том, чтобы по значениям функции \(f(x)\) в нескольких точках отрезка восстановить ее значения в остальных точках этого отрезка. Разумеется, такая задача допускает сколь угодно много решений. Задача интерполирования возникает, например, в том случае, когда известны результаты измерения \(y_h= f(x, k)\) некоторой физической величины \(f(x)\) в точках \(x_k, k = 0, 1, ..., n\), и требуется определить ее значения в других точках. Интерполирование используется также при сгущении таблиц, когда вычисление значений \(f(x)\) трудоемко. Иногда возникает необходимость приближенной замены или аппроксимации данной функции другими функциями, которые легче вычислить. В частности, рассматривается задача о наилучшем приближении в нормированном пространстве \(H\), когда заданную функцию \(f\in H\) требуется заменить линейной комбинацией \(\phi\) заданных элементов из \(H\) так, чтобы отклонение \(||f—\phi||\) было минимальным. Результаты и методы теории интерполирования и приближения функций нашли широкое применение в численном анализе, например при выводе формул численного дифференцирования и интегрирования, при построении сеточных аналогов задач математической физики [1].

Для того чтобы рассмотреть интерполяцию, сгенерируем данные. Т.е. сгенерируем массив узлов интерполяционной сетки x_data и значений y_data некоторой функции \(f\) в узлах этой сетки.

import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline

L = 0
R = np.pi
n_points = 10 # при 63 уже ломается 
f = np.sin


def plot_problem(ax, x_data, y_data):
    ax.scatter(x_data, y_data, marker="x", color="red")
    ax.set_xlabel("x")
    ax.set_ylabel("y")
    

x_data = np.linspace(L, R, n_points - 1) # данные для интерполяции
y_data = f(x_data)                       # данные для интерполяции


x = np.linspace(L, R, 100)    # данные для построения графика
y = f(x)                      # данные для построения графика

fig, ax = plt.subplots()
ax.plot(x, y)
plot_problem(ax, x_data, y_data)
ax.set_title("Исходные данные")
ax.legend(["Интерполируемая функция", "Данные для интерполяции"])
plt.show()

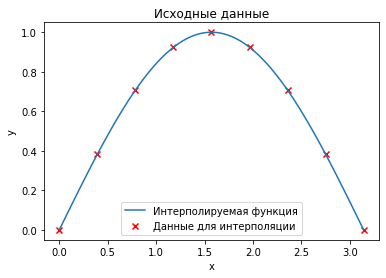
Теперь когда данные готовы, осталось произвести интерполяцию. Методов интерполяции существует очень много. Рассмотрим полиномиальную интерполяцию и сплайн интерполяцию.

Полиномиальная интерполяция

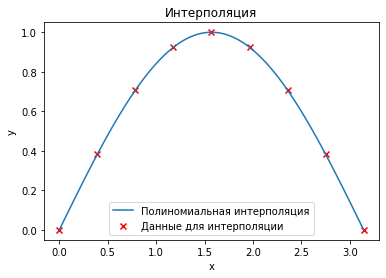
Полиномиальная интерполяция основывается на том факте, что существует единственный полином \(P_{N}(x) = a_0 + a_1 x + \cdots + a_{N} x ^ N \) степени \(N\), проходящий через точки \(\{(x_1, y_1), ..., (x_{N + 1}, y_{N + 1})\}\), если \(x_i \neq x_j \quad \forall i, j = 1, \cdots, N + 1, \quad i \neq j\).

Недостатком полиномиальной интерполяции является её нестабильность. Полиномиальная интерполяция проявляет себя очень плохо при больших \(N\).

from scipy import interpolate

poly = interpolate.KroghInterpolator(x_data, y_data)
y_poly = poly(x)

fig, ax = plt.subplots()
ax.plot(x, y_poly)
plot_problem(ax, x_data, y_data)
ax.legend(["Полиномиальная интерполяция", "Данные для интерполяции"])
ax.set_title("Интерполяция")

Text(0.5, 1.0, 'Интерполяция')

Сплайн интерполяция

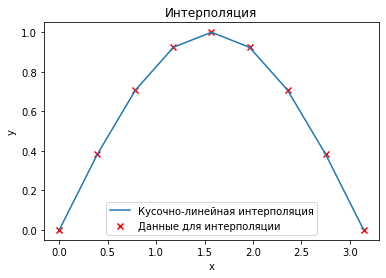
Интерполирование многочленом … на всем отрезке \([a, b]\) с использованием большого числа узлов интерполяции часто приводит к плохому приближению, что объясняется сильным накоплением погрешностей в процессе вычислений. Кроме того, из-за расходимости процесса интерполяции увеличение числа узлов не обязано приводить к повышению точности. Для того чтобы избежать больших погрешностей, весь отрезок \([a, b]\) разбивают на частичные отрезки и на каждом из частичных отрезков приближенно заменяют функцию \(f(х)\) многочленом невысокой степени (так называемая кусочно-полиномиальная интерполяция). Одним из способов интерполирования на всем отрезке является интерполирование с помощью сплайн-функций. Сплайн-функцией или сплайном называют кусочно-полиномиальную функцию, определенную на отрезке \([a, b]\) и имеющую на этом отрезке некоторое число непрерывных производных [1].

linear = interpolate.interp1d(x_data, y_data, kind="linear")
y_linear = linear(x)

fig, ax = plt.subplots()
ax.plot(x, y_linear)
plot_problem(ax, x_data, y_data)
ax.legend(["Кусочно-линейная интерполяция", "Данные для интерполяции"])
ax.set_title("Интерполяция")

Text(0.5, 1.0, 'Интерполяция')

cubic = interpolate.interp1d(x_data, y_data, kind="cubic")
y_cubic = cubic(x)

fig, ax = plt.subplots()
ax.plot(x, y_cubic)
plot_problem(ax, x_data, y_data)
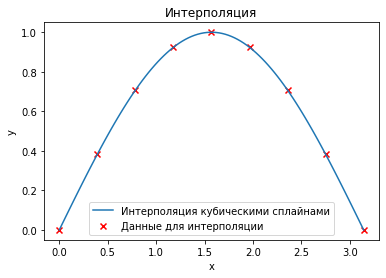
ax.legend(["Интерполяция кубическими сплайнами", "Данные для интерполяции"])
ax.set_title("Интерполяция")

Text(0.5, 1.0, 'Интерполяция')

Аппроксимация функций

Задача аппроксимации функции очень похожа на задачу интерполирования, но в интерполировании обычно ставится целью поиск такой функции \(\phi\), которая в точности проходит через известные нам точки \((x_i, y_i)\), где \(y_i = f(x_i), i = 1, ..., N\), а при аппроксимации допускается отклонение функции \(\phi\) от этих точек.

В ряде ситуаций, значение исходной функции \(f\) в точках \(x_i, i=1,...,N\) может быть известно не точно, а в пределах какой-то погрешности или с точностью до какой-то случайной величины, т.е., например, \(y_i = f(x_i) + \varepsilon_i, \, i = 1, ..., N\). В таком случае такое строгое требование на то, чтобы наше решение \(\phi(x)\) в точности проходило через все точки \((x_i, y_i), i=1, ..., N\) не имеет большого смысла и может быть ослаблено, например, до поиска такой функции \(\phi\) из определенного класса функций, которая меньше всего отклоняется от значений \((x_i, y_i), i=1,..., n\).

Пусть, аппроксимирующая функция дана в параметризованном виде и задача аппроксимации ставится следующим образом:

\[ \sum_{i=1}^{N}||\phi_p(x_i) - y_i||^2 \sim \min_{p\in D}. \]

Иными словами требуется найти такие параметры \(p\), что функция \(\phi_p(x)\) наименее всего отклоняется от точек \((x_i, y_i), i=1, ..., N\) в среднеквадратичном смысле.

Note

В общем случае, и \(x_i\), \(y_i\) и \(p\) — здесь векирные величины.

При такой постановке часто выделяют линейную и нелинейную аппроксимации. Аппроксимация является линейной, если \(\phi_p(x)\) линейно зависит от параметров \(p\), не линейной в ином случае.

Note

Аппроксимация функций реализована во множестве других библиотек, таких как statsmodels, scikit-learn и некоторых других.

Линейная аппроксимация

Разберем в качестве примера полиномиальную аппроксимацию. Для начала сгенерируем данные.

import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline

def f(x):
    return 0.5 + 2 * x + 3 * x * x

def plot_problem(ax, x_true, y_true, x_data, y_data):
    ax.scatter(x_data, y_data)
    ax.plot(x_true, y_true, 'r')
    ax.set_xlabel("x")
    ax.set_xlabel("y")
    ax.set_title("Аппроксимация")



N = 100
sigma = 0.2
x_data = np.random.uniform(low=0, high=1, size=N)
y_data = f(x_data) + np.random.normal(loc=0, scale=sigma, size=N)

x = np.linspace(0, 1, 100) # чтобы строить график
y = f(x)                   # чтобы строить график


fig, ax = plt.subplots()
plot_problem(ax, x, y, x_data, y_data)
ax.legend(["Исходная функция", "Данные для апроксимации",])

<matplotlib.legend.Legend at 0x1a87e7be7f0>

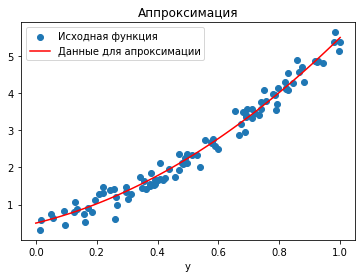
В ячейке выше, мы сгенерировали массив x_data случайных значений в интервале \([0, 1]\). На основе него и функции f мы сгенерировали массив y_data, который представляют из себя сумму значений функции f в точках с координатами x_data и случайного шума, распределенного по Гауссу с нулевым средним и дисперсией sigma.

На графике мы построили набор получившихся точек и исходную функцию f. Теперь попробуем приблизить её линейной функцией \(\phi_1(x) = \alpha_1 + \beta_1 x\) методом наименьших квадратов, т.е. мы хотим решить задачу минимизации невязки R, где невязка для заданных параметров \(\alpha_1\) и \(\beta_1\) задаётся суммой квадратов отклонений функции \(\phi_1(x)\) в точках \(x_i\) от \(y_i\):

\[ R_1 = \sum_{i=1}^{N} (\phi_1(x_i) - y_i) ^ 2 = \sum_{i=1}^{N} (\alpha_1 + \beta_1 x_i - y_i) ^ 2 \sim \min_{\alpha_1, \beta_1}, \]

где \(x_i\) соответствует x_data[i], а \(y_i\) соответствует y_data[i].

Решить эту задачу можно методом scipy.linalg.lstsq. Он позволяет найти такой \(x\), который минимизирует невязку СЛАУ \(A x = b\) методом наименьших квадратов, т.е. \(x = \text{argmin}_{x\in\mathbb{R}^2} || A x- b|| ^ 2\). В нашей задаче этот \(x\) представляет собой вектор параметров \(\alpha_1\) и \(\beta_1\). Нам необходимо составить матрицу \(A\) и вектор \(b\) таким образом, чтобы невязка \(|| A x - b || ^ 2\) для заданного вектора \(x = \begin{pmatrix} \alpha_1 \\ \beta_1 \end{pmatrix}\) совпадала с \(R_1\). Для этого составим матрицу \(A\) следующего вида:

\[\begin{split} A = \begin{pmatrix} 1 & x_0 \\ 1 & x_1 \\ \vdots & \vdots \\ 1 & x_n \end{pmatrix}, \end{split}\]

а в качестве вектора \(b\) возьмем наш массив y_data и заметим, что невязка уравнения

\[\begin{split} \begin{pmatrix} 1 & x_0 \\ 1 & x_1 \\ \vdots & \vdots \\ 1 & x_n \end{pmatrix} \begin{pmatrix} \alpha_1 \\ \beta_1 \end{pmatrix} = \begin{pmatrix} y_0 \\ y_1 \\ \vdots \\ y_n \end{pmatrix} \end{split}\]

совпадает с искомой минимизируемой величиной \(R_1\).

from scipy import linalg

A = x_data[:, np.newaxis] ** [0, 1]
b = y_data

sol, _, _, _ = linalg.lstsq(A, b)
alpha_1, beta_1 = sol
y_approx = alpha_1 + beta_1 * x
print(alpha_1, beta_1)


fig, ax = plt.subplots()
plot_problem(ax, x, y, x_data, y_data)
ax.plot(x, y_approx)
ax.legend(["Исходная функция", "Аппроксимация прямой", "Данные для аппроксимации"])

-0.1275795291100632 5.140306459685289

<matplotlib.legend.Legend at 0x1a87e848160>

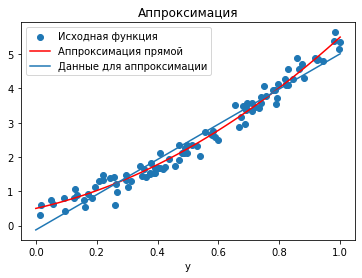
Как видно, аппроксимирующая функция подстроилась под набор точек, но не идеально. Это связано с тем, что мы искали решение в классе линейных функций, а искомая функция имеет квадратичное слагаемое. Расширим класс наших функций. Будем искать решение в виде функции \(\phi_2(x) = \alpha_2 + \beta_2 x + \gamma_2 x^2\).

Соответствующая СЛАУ с нужной нам невязкой будет иметь вид:

\[\begin{split} \begin{pmatrix} 1 & x_0 & x_0 ^ 2\\ 1 & x_1 & x_1 ^ 2\\ \vdots & \vdots & \vdots \\ 1 & x_n & x_n^2 \end{pmatrix} \begin{pmatrix} \alpha_2 \\ \beta_2 \\ \gamma_2 \end{pmatrix} = \begin{pmatrix} y_0 \\ y_1 \\ \vdots \\ y_n \end{pmatrix}. \end{split}\]

A = x_data[:, np.newaxis] ** [0, 1, 2]
b = y_data

sol, _, _, _ = linalg.lstsq(A, b)
alpha_2, beta_2, gamma_2 = sol
y_approx = alpha_2 + beta_2 * x + gamma_2 * x * x
print(alpha_2, beta_2, gamma_2)

fig, ax = plt.subplots()
plot_problem(ax, x, y, x_data, y_data)
ax.plot(x, y_approx)
ax.legend(["Исходная функция", "Аппроксимация квадратным трехчленом", "Данные для аппроксимации"])

0.48596480315036283 1.9274612379660878 3.101950199682327

<matplotlib.legend.Legend at 0x1a87e8c1250>

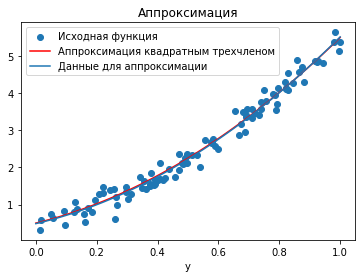
Квадратный трехчлен гораздо ближе проходит к исходной функции.

Вообще говоря, таким способом можно искать решение в виде линейной комбинации любых функций \(\varphi(x) = c_1\varphi_1(x) + \cdots + c_k\varphi_k(x)\). Соответствующая матрица \(A\) будет иметь вид

\[\begin{split} A = \begin{pmatrix} \varphi_1(x_1) &\cdots & \varphi_k(x_1) \\ \vdots & \ddots & \vdots \\ \varphi_1(x_N) &\cdots & \varphi_k(x_N) \end{pmatrix}. \end{split}\]

А конкретно для полиномиальных функций существует функция np.polyfit.

Note

Все вышерассмотренные случаи представляют собой линейную аппроксимацию, т.к. аппроксимирующая функция линейно зависила от подбираемых параметров (коэффициентов).

Нелинейная аппроксимация

Сгенерируем данные для нелинейной аппроксимации.

import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline

def f(x):
    return 2*np.exp(-3*x) + 4

def plot_problem(ax, x_true, y_true, x_data, y_data):
    ax.scatter(x_data, y_data)
    ax.plot(x_true, y_true, 'r')
    ax.set_xlabel("x")
    ax.set_xlabel("y")
    ax.set_title("Аппроксимация")



N = 50
sigma = 0.2
x_data = np.random.uniform(low=0, high=1, size=N)
y_data = f(x_data) + np.random.normal(loc=0, scale=sigma, size=N)

x = np.linspace(0, 1, 100) # чтобы строить график
y = f(x)                   # чтобы строить график


fig, ax = plt.subplots()
plot_problem(ax, x, y, x_data, y_data)
ax.legend(["Исходная функция", "Данные для апроксимации",])

<matplotlib.legend.Legend at 0x1a87e928e80>

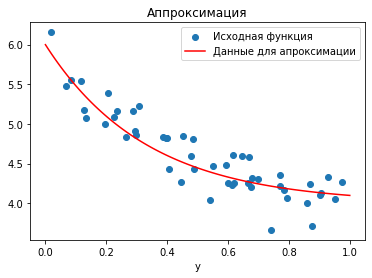
Будем искать нашу функцию в виде

\[ \phi_{\alpha, \beta, \gamma}(x) = \alpha e^{\beta x} + \gamma, \]

и попробуем восстановить значения параметров \(\alpha, \beta\) и \(\gamma\) из сгенерированных данных. Аппроксимация не линейна, т.к. \(\phi\) нелинейно зависит от параметра \(\beta\). Метод optimize.curve_fit позволяет искать приближенное решение задачи нелинейной аппроксимации.

Чтобы воспользоваться этим методом, необходимо определить функцию, которая первым своим аргументом принимает \(x\) (может быть скаляром, а может быть и вектором), а остальными аргументами принимает параметры \(p\). В примере ниже это функция f_approx.

from scipy import optimize

def f_approx(x, alpha, beta, gamma):
    return alpha * np.exp(beta * x) + gamma

p, _ = optimize.curve_fit(f_approx, x_data, y_data, p0=[3, -6, 10])

y_approx = f_approx(x, *p)

fig, ax = plt.subplots()
plot_problem(ax, x, y, x_data, y_data)
ax.plot(x, y_approx, color="g")
ax.legend(["Исходная функция", "Аппроксимация", "Данные для аппроксимации"])

print("""
Найденные параметры: 
alpha: {:.3f},
beta: {:.3f},
gamma: {:.3f}
""".format(*p)
)

Найденные параметры: 
alpha: 2.126,
beta: -2.201,
gamma: 3.809

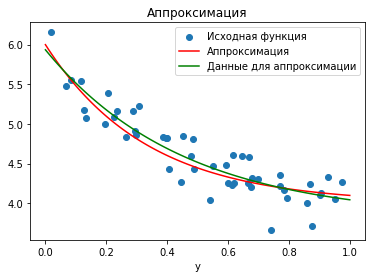
В случае нелинейной аппроксимации следует проявлять особую осторожность, т.е. среднеквадратичное отклонение минимизируется численными методами и начальное предположение о значениях параметров \(p0\) играет большую роль: при не удачном \(p0\) алгоритм может сойтись не туда или вообще не сойтись.

Список литературы

1(1,2,3)

Гулин А.В. Самарский А.А. Численные методы. М. Наука, 1989. ISBN 5-02-013996-3.

2

Брайан К. Джонс Дэвид Бизли. Python. Книга рецептов. М. ДМК Пресс, 2019. ISBN 978-5-97060-751-0.

previous

Линейная алгебра

next

Определенные интегралы