.ipynb .pdf

Contents

Домашнее задание №3

Это домашнее задание посвящено численному и математическому моделированию.

Вашу программу следует разделить на следующие логические этапы.

1. Чтение конфигурации из конфигурационного файла (физические параметры системы, коэффициенты уравнения, параметры методов решения задачи) и т.д.;

2. Получение численного решения задачи при заданных параметрах;

3. Визуализация полученного решения.

Ваша задача заключается не только в программировании, но и в анализе самой задачи и её решений, которые могут иметь качественно разный характер при разных параметрах. Необходимо подготовить к моменту сдачи несколько конфигурационных файлов, демонстрирующих максимально разнообразие. Конфигурационные файлы разумно представить в виде JSON.

Численное моделирование следует осуществлять на основе методов библиотеки SciPy, а не реализовывать численные методы самостоятельно. В целях визуализации допускается использовать любую библиотеку. На каждом графике должны быть подписаны оси (ax.set_xlabel и т.д.). Если в одних осях построены графики нескольких функций, то следует составить легенду (ax.set_legend).

Желательно протестировать вашу программу. Если решение вашей задачи при каких-то параметрах очевидно, то следует проверить, что ваша программа способно его найти (в пределах погрешности).

1. Вычисление моментов инерции

Пусть дано тело с плотностью \(\rho(x, y, z)\) в пределах области \(D\).

Найти:

1. Его центр масс

2. Тензор инерции

3. Его главные оси

И визуализировать это тело с его главными осями.

Предусмотреть тела следующих форм: параллелепипед, сфера, цилиндр, конус и тор.

2. Задача двух тел

Записать систему дифференциальных уравнений для задачи двух тел и реализовать её численное решение. Построить траектории этих тел (опционально можно визуализировать решение анимацией).

3. Тепловое равновесие

Рассмотрим стержень длинны \(l\), на концах которого поддерживаются температуры \(T_0\) и \(T_l\) соответственно.

Если направить ось \(Ox\) вдоль длинны стержня как на рисунке выше и считать, что температура зависит только от координаты \(x\) и что стержень теплоизолирован по его длине, то распределение температуры по длине стержня при достижении теплового равновесия описывается уравнением

\[\begin{split} \begin{cases} \dfrac{d}{dx}(\rho(x)\dfrac{dT}{dx}) = 0 \\ T\big|_{x=0} = T_0 \\ T\big|_{x=l} = T_l. \end{cases} \end{split}\]

Здесь \(\rho\) — коэффициент теплопроводности. В общем случае этот коэффициент зависит от \(x\), а в случае однородного стержня \(\rho(x)\) — константа.

4. Осциллятор Ван дер Поля

Реализовать численное решение уравнения Ван дер Поля

\[\begin{split} \begin{cases} y'' - k (1- y^2)y' + y = 0 \\ y\big|_{t=0} = y_0 \\ y'\big|_{t=0} = y'_0 \end{cases} \end{split}\]

Построить график решения в осях \((t, y)\) и \((y, y')\). Исследовать решение в зависимости от различных начальных условий, значений коэффициента \(k\).

5. Уравнение Дуффинга

В теории колебаний одним из наиболее известных нелинейных уравнений является уравнение Дуффинга, которое с учётом внешней силы записывается в виде

\[ \ddot{x} + 2\delta \dot{x} + \alpha x + \beta x^3 = B \sin(\omega t) \]

Пусть \(\delta=0.05\), \(\alpha=1\), \(\beta=1\), \(\omega=1\)

6. Хищник-жертва

Пусть \(x\) — плотность популяции жертвы, \(y\) — плотность популяции хищника, тогда, согласно модели Лотки-Вольтерра, модели хищник-жертва, можно записать следующие уравнения:

\[\begin{split} \begin{cases} \dot{x} = ax - bxy\\ \dot{y} = cxy - dy \end{cases}, \end{split}\]

где \(a, b, c\) и \(d\) положительные константы. Коэффициент \(a\) описывает интенсивность размножения жертв, \(b\) — выедание хищниками жертв, \(c\) — увеличение биомассы хищников за счет выедания жертв, \(d\) — интенсивность естественной смерти хищников.

Реализовать численное решение этой системы ОДУ и подобрать такие начальные плотности популяций и коэффициенты \(a, b, c\) и \(d\), чтобы наблюдались периодические колебания, описывающие совместное проживание популяций жертв и хищников.

7. Аттрактор Лоренца

Рассмотрим систему нелинейных ОДУ

\[\begin{split} \begin{cases} \dot{x} = \sigma (y - x)\\ \dot{y} = x (r - z) - y\\ \dot{z} = xy - bz. \end{cases} \end{split}\]

Реализовать численное решение этой системы, продемонстрировать странный аттрактор.

8. Заряды в электростатическом поле

Пусть дано внешнее электростатическое поле, потенциальная энергия взаимодействия которого с зарядом \(q\) имеющим координаты \(\vec{r}=(x, y, z)\) имеет вид:

\[ W_q(\vec{r}) = kq(x^2 + \dfrac{y^2}{4} + \dfrac{z^2}{16}). \]

Предположим в это поле запускаются \(N\) частиц с положительными зарядами \(q_1, \cdots, q_N\). Будем считать, что зависимость потенциальной энергии такой системы зарядов от положений этих зарядов \(\vec{r_1}, ..., \vec{r_N}\) имеет вид

\[ W(\overrightarrow{r_1}, ..., \overrightarrow{r_N}) = \sum_{i=1}^N W_{q_i}(\overrightarrow{r_i}) + \dfrac{1}{2}\sum_{i\neq j}k \dfrac{q_i q_j}{r_{ij}}, \]

где \(r_{ij}\) расстояние от \(i\) до \(j\) заряда. Т.е. потенциальная энергия системы является суммой энергии взаимодействия каждого заряда с электростатическим полем и энергией взаимодействия частиц между собой.

Найти положение равновесия такой системы, считая, что оно достигается при минимальной потенциальной энергии:

\[ W(\overrightarrow{r_1}, ..., \overrightarrow{r_N}) \sim \min_{\overrightarrow{r_1}, ..., \overrightarrow{r_N}}. \]

Визуализировать частицы в найденном положении равновесия.

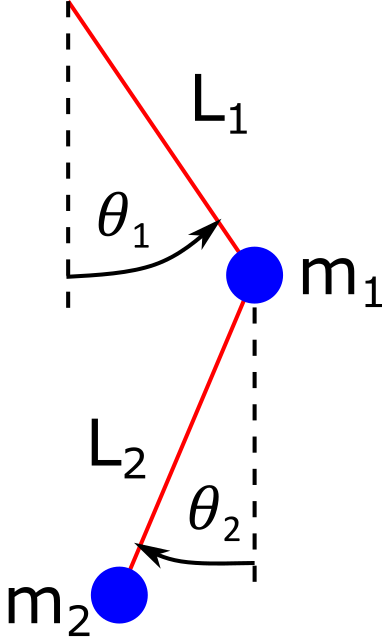
9. Двойной маятник

Смоделируйте поведение двойного маятника.

Состояние системы в любой момент времени может быть описано углами \(\theta_1\) и \(\theta_2\) и угловыми скоростями \(\omega_1 = \dot{\theta_1}\) и \(\omega_2 = \dot{\theta_2}\). Если выбрать углы в соответствии с рисунком выше, то уравнения движения имеют вид

\[\begin{split} \begin{cases} \varepsilon_1 = \dfrac{-g(2m_1 + m_2)\sin\theta_1-gm_2\sin(\theta_1 - 2\theta_2) - 2\sin(\theta_1 - \theta_2)m_2(\omega_2^2L_2 + \omega_1^2l_1\cos(\theta_1 - \theta_2))}{L_1(2m_1 + m_2 - m_2 \cos(2\theta_1 - 2 \theta_2))}, \\ \varepsilon_2 = \dfrac{2\sin(\theta_1 - \theta_2)(\omega_1^2L_1(m_1 + m_2) + g(m_1 + m_2)\cos\theta_1 + \omega_2^2 L_2 m_2 \cos(\theta_1 - \theta_2))}{L_1(2m_1 + m_2 - m_2 \cos(2\theta_1 - 2 \theta_2))}. \end{cases} \end{split}\]

Здесь \(\varepsilon_1 = \ddot{\theta}_1\) и \(\varepsilon_2 = \ddot{\theta}_2\) — угловые ускорения.

10. Два маятника на пружине

Рассмотрим механическую систему, состоящую из двух пружинных маятников, соединенных между собой ещё одной пружиной. Предположим, что в состоянии покоя системы все три пружины не испытывают деформаций.

Теперь предположим, что эту систему вывели из состояния покоя, сместив грузики из положений равновесий и придав им некоторые скорости. Пусть \(x_1\) — смещение первого грузика вправо относительно его положения равновесия, \(x_2\) — смещение второго грузика вправо относительно его положения равновесия, тогда уравнения движения имеют вид

\[\begin{split} \begin{cases} ma_1 = -k_1 x_1 + k(x_2 - x_1),\\ ma_2 = -k_2 x_2 - k(x_2 - x_1), \end{cases} \end{split}\]

где \(a_1 = \ddot{x}_1\) и \(a_2 = \ddot{x}_2\) — ускорения грузиков. Смоделировать поведение такой системы.

11. Заряд в электромагнитном поле

Точечный заряд движется в постоянном электромагнитном поле, т.е. него действует сила Лоренца

\[ \overrightarrow{F} = q(\overrightarrow{E} + [\overrightarrow{v} \times \overrightarrow{B}]). \]

Здесь \(q\) — величина заряда, \(\overrightarrow{E}=\overrightarrow{E}(\vec{r})\) и \(\overrightarrow{B}=\overrightarrow{B}(r)\) — напряженности электрического и магнитного полей, \(\vec{r}\) и \(\vec{v}\) — радиус-вектор положения частицы и вектор мгновенной скорости частицы.

Пренебрегая силой тяжести, смоделировать полет заряда в таком поле решив уравнения движения

\[ m\vec{a} = \overrightarrow{F}, \]

при некоторых начальных условиях \(\vec{r}\big|_{t=0} = \vec{r}_0, \, \vec{v}\big|_{t=0} = \vec{v}_0\). Предусмотреть равномерные (\(\overrightarrow{E}(\vec{r}) = \overrightarrow{E}_0\), \(\overrightarrow{B}(\vec{r}) = \overrightarrow{B}_0\)) и радиальные (\(\overrightarrow{E}(\vec{r}) = \vec{r}||\overrightarrow{E}||/||\vec{r}||\), \(\overrightarrow{B}(\vec{r}) = \vec{r}||\overrightarrow{B}||/||\vec{r}||\)) электрические и магнитные поля.

12. Ядерный реактор

Динамика ядерного реактора в простейшей модели описывается системой уравнений на мощность \(N\) и температуру \(T\) реактора:

\[\begin{split} \begin{cases} \dfrac{dN}{dt} = - \dfrac{\alpha (T - T_1)}{\tau}N, \\ C \dfrac{dT}{dt} = N - k (T-T_0), \end{cases} \end{split}\]

где \(\tau\) — время жизни одного поколения нейтронов, \(\alpha > 0\) — реактивность реактора, \(C\) — теплоемкость реактора, \(T_1\) — температура окружающей среды, \(T_0 < T_1\) — температура охладителя реактора, \(k\) — коэффициент теплоотдачи реактора.

13. Химический реактор

Реактор представляет собой открытую систему полного перемешивания с непрерывным тепло- и массообменом с окружающей средой. Химическая реакция протекает гомогенно с выделением тепла, которое отводится как потоком вещества, так и теплопередачей через стенки реактора. Зависимость скорости реакции от концентрации реагента и температуры определяется законом действующих масс Аррениуса. В этой простейшей модели динамика реактора описывается системой уравнений на концентрацию реагента \(x\) и его температуру \(y\):

\[\begin{split} \begin{cases} \dfrac{dx}{dt} = -x e^{-1/y} + \lambda (x_0 - x), \\ \dfrac{dy}{dt} = -x e^{-1/y} + \mu (y_0 - y), \end{cases} \end{split}\]

где \(x_0\) –– концентрация подающегося реагента, \(y_0\) – равновесная температура реактора при потушенной реакции, \(\lambda\) – скорость вывода реагента из реактора, \(\mu\) – скорость охлаждения за счёт вывода реагента и отвода тепла.

previous

Пример

next

Создание скриптов. Работа с IDE