Contents

Решение ОДУ

Решение ОДУ

Подмодуль scipy.integrate содержит в себе множество методов решения систем обыкновенных дифференциальных уравнений (ОДУ, ordinary differential equation, ODE).

Т.к. везде ниже будут строиться графики полученного и точного решений уравнения, определим функцию для построения графиков этих решений.

from matplotlib import pyplot as plt
def plot(ax, x, exact_sol, sol_x, sol_y, xlabel="t", s="r."):
    ax.plot(x, exact_sol(x), "b")
    ax.plot(sol_x, sol_y, s)
    ax.set_xlabel(xlabel)
    ax.set_ylabel("y")
    ax.legend(["Точное решение", "Приближенное решение"])

Задача Коши

Функция scipy.integrate.solve_ivp (solve initial value problem) позволяет численно решать задачу Коши вида

\[\begin{split} \begin{cases} \dfrac{dy}{dt} = f(t, y) \\ y(t_0) = y_0. \end{cases} \end{split}\]

Предполагается, что в общем случае \(y=y(t)\) является векторной и решается система обыкновенных дифференциальных уравнений.

\[\begin{split} \begin{cases} \dot{y}_1 = f_1(t, y_1, \cdots, y_n), \\ \cdots \\ \dot{y}_n = f_n(t, y_1, \cdots, y_n), \\ y_1(t_0) = y_{10}, \\ \cdots \\ y_n(t_0) = y_{n0}. \end{cases} \end{split}\]

Note

Чтобы численно решить уравнение \(n\)-го порядка, необходимо свести его к системе из \(n\) уравнений первого порядка.

В качестве самого простого примера, решим уравнение

\[\begin{split} \begin{cases} y' = y, \\ y(0) = 0. \end{cases} \end{split}\]
import numpy as np
from scipy import integrate
from matplotlib import pyplot as plt


def f(t, y):
    return y

def exact_solution(t):
    return np.exp(t)

y_0 = [1]
t_0 = 0
t_final = 3
sol = integrate.solve_ivp(f, (t_0, t_final), y_0)


fig, ax = plt.subplots()
fig.set_size_inches((10, 9))
plot(ax, np.linspace(t_0, t_final, 100), exact_solution, sol.t, sol.y[0], s="r-")
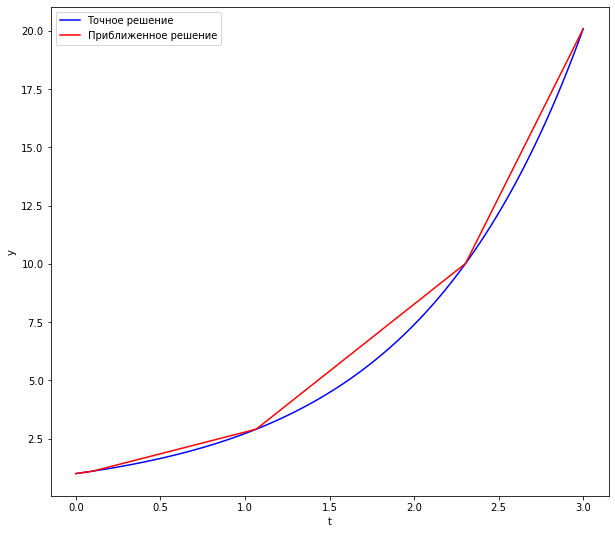
../_images/scipy_ODE_3_0.png

На что следует обратить внимание.

  • Хоть правая часть уравнения и не зависит явным образом от \(t\), функция f(t, x) все равно объявляется с первым параметром t;

  • Функция \(y=y(t)\) в этом уравнение скалярная, но мы представляем её в виде векторной функции \(f:\mathbb{R}^1 \to \mathbb{R}^1\);

  • Помимо функции правой части искомого ОДУ, функция scipy.integrate.solve_ivp принимает отрезок t_span (\([t_0, t_{\text{final}}])\), на котором решается уравнение, и начальные условия в виде вектора \(y_0\);

  • В итоговом решение компонента sol.t соответствует значениям по оси t, а sol.y значениям полученного решения в точках из sol.t. Т.к. \(y\) считается векторной функцией, то sol.е — матрица, каждая строка которой соответствует компоненте вектора \(y\), а каждый столбец значению \(t\) из sol.t;

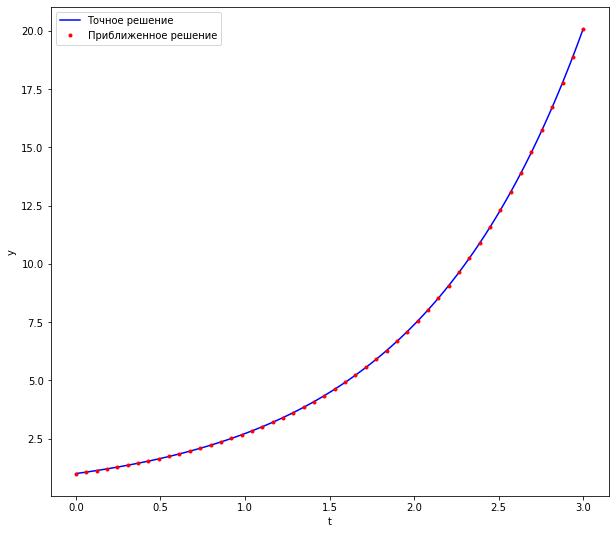
  • Для данного уравнения функция scipy.integrate.solve_ivp выдала решение, содержащее совсем небольшое количество значений \(t\). Можно попросить у этой функции получить решение на заданной сетке \(t\).

sol = integrate.solve_ivp(f, (t_0, t_final), y_0, t_eval=np.linspace(t_0, t_final, 50))

fig, ax = plt.subplots()
fig.set_size_inches((10, 9))
plot(ax, np.linspace(t_0, t_final, 100), exact_solution, sol.t, sol.y[0])
../_images/scipy_ODE_5_0.png

Выбор метода решения ОДУ

Решение таких систем ОДУ отнюдь не тривиально. Разработано множество методов их решения и ряд из них “зашит” в подмодуле scipy.integrate, среди которых:

  • Явные ме́тоды Ру́нге — Ку́тты 2-го (RK23), 4-го (RK45) и 8-го (DOP853) порядков;

  • Неявный метод Руне — Кутты 5-го порядка Radau;

  • Неявные методы BDF и LSODA.

Основным критерием выбора является жесткость системы ОДУ: явные методы плохо проявляют себя на жестких системах. SciPy рекомендует использовать по умолчанию метод RK45 и если он плохо/долго сходится переключаться на метод Radau иди BDF.

Краевая задача

Функция scipy.integrate.solve_bvp (Solve boundary value problem) предназначена для решения системы ОДУ с краевыми условиями

\[\begin{split} \begin{cases} \dfrac{dy}{dx} = f(x, y) \\ y(a) = y_a \\ y(b) = y_b. \end{cases} \end{split}\]

В качестве аргументов функция solve_bvp принимает:

  • функцию f, задающую правую часть уравнения,

  • функцию bc (сокращение от boundary condition), задающую невязку для граничных условий,

  • массив x, определяющий сетку значений независимой переменной \(x\),

  • массив y, задающий “догадку” об итоговом решении \(y = y(x)\).

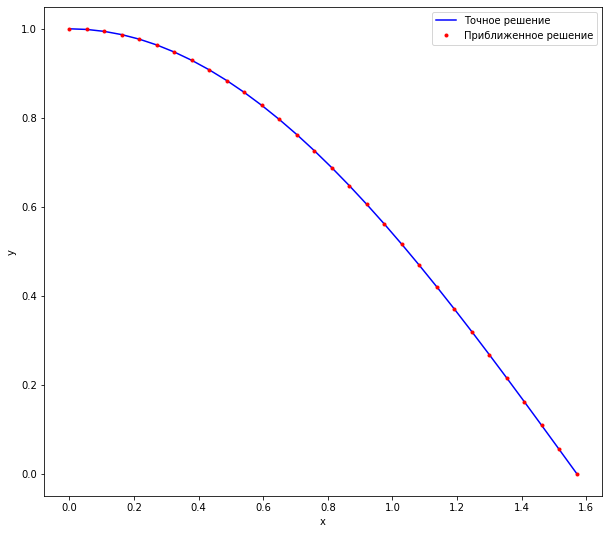
В качестве примера решим уравнение

\[\begin{split} \begin{cases} y'' + y = 0 \\ y(0) = 1 \\ y(\frac{\pi}{2}) = 0, \end{cases} \end{split}\]

на отрезке \(x \in [0, \frac{\pi}{2}]\). Чтобы это сделать, необходимо свести это уравнение второго порядка к системе уравнений первого порядка. Для этого введем обозначения \(z_1 = y\) и \(z_2 = y'\). Тогда систему выше можно записать в виде

\[\begin{split} \begin{cases} z_1' = z_2 \\ z_2' = - z_1 \\ z_1(0) = 1 \\ z_1(\frac{\pi}{2}) = 0. \end{cases} \end{split}\]
import numpy as np
from scipy import integrate
from matplotlib import pyplot as plt


def f(x, z):
    return [
        z[1],
        -z[0]
    ]

def R(za, zb):
    return np.array([za[0] - 1, zb[0]]) 

def exact_solution(x):
    return np.cos(x)

a, b = 0, np.pi/2
N = 30
x = np.linspace(a, b, N)
z_guess = np.zeros((2, N), dtype=float)

sol = integrate.solve_bvp(f, R, x, z_guess)

fig, ax = plt.subplots()
fig.set_size_inches((10, 9))
plot(ax, x, exact_solution, sol.x, sol.y[0], xlabel="x")
../_images/scipy_ODE_8_0.png

previous

Определенные интегралы

next

Оптимизация