Contents

Знакомство с NumPy

Знакомство с NumPy

Первая сторонняя библиотека, с которой мы познакомимся — NumPy (Numerical Python).

Библиотека NumPy предоставляет доступ к многомерным массивам однородных данных (одного типа, обычно числа), подобным массивам C/C++, и к методам их обработки. На самом деле, под капотом эти самые массивы реализованы с помощью динамических массивов C/C++, которые в отличие от списков, хранят непосредственно данные, а не указатели на них.

Зачем нужен NumPy

Необходимость в специальной библиотеке для работы с большими массивами чисел, возникает из-за скорости работы python. За гибкость, выразительность, динамическую типизацию и многие другие достоинства, python приходится платить скоростью: код написанные на python, практически всегда будет работать медленнее, чем аналогичный код, написанный на C/C++. Проще всего заметить на примере циклов.

#include <iostream>
#include <chrono>
#include <vector>
#include <random>
#define N 10000000

int main(){
    // Готовим генератор случайных чисел
    std::random_device rd;
    std::mt19937 gen(rd());
    std::uniform_real_distribution<> dis(-1.0, 1.0);
    
    // Создаём массивы случайных чисел
    std::vector<double> a(N), b(N), c(N);
    for(int i=0; i < N; ++i){
        a[i] = dis(gen);
        b[i] = dis(gen);
    }
	
    // Измеряем время сложения векторов
    auto t1 = std::chrono::high_resolution_clock::now();
    
    for(int i = 0; i < N; ++i)
        c[i] = a[i] + b[i];
        
    auto t2 = std::chrono::high_resolution_clock::now();
    
    auto ms_int = std::chrono::duration_cast<std::chrono::milliseconds>(t2 - t1);
    std::cout << ms_int.count() << " ms";
}

import time
from random import uniform


N = 10000000

# Создаём списки случайных чисел
a = [uniform(-1, 1) for i in range(N)] # новый синтаксис, список случайных чисел
b = [uniform(-1, 1) for i in range(N)]
c = [0.] * N 

# Измеряем время сложения этих списков
t1 = time.time()

for i in range(N):
    c[i] = a[i] + b[i]
        
t2 = time.time()
print(f"{(t2 - t1) * 1000} ms") # time() - время в секундах

Note

Документацию по модулю time можно найти здесь, а по модулю random здесь.

Два исходных кода выше делают похожие вещи, но на C/C++ и python соответственно. Оба создают массивы случайных чисел и измеряют время, необходимое на их сложение. Я сохранил эти исходные коды в файлы loops.cpp и loops.py и исполнял этот код на одной и той же машине, следующими командами. Флаг -O0 сообщает компилятору, что компилировать надо в режиме debug, что отключает огромное количество оптимизаций.

g++ loops.cpp -O0 -o loops
loops.exe
python loops.py

В среднем, я получил следующие результаты.

python

C/C++

2425 ms

87 ms

Note

Вообще говоря, на эти цифры может повлиять огромное количество факторов, в том числе и случайных. Тем не менее разница настолько явная, что качественная картина ясна: циклы в C/C++ работают заметно быстрее, чем в python.

“Среднее” приложение на python не сталкивается с обработкой больших объемов данных и обычно разница в производительности компенсируется затраченным на реализацию алгоритма временем. Но научные вычисления очень часто представляют собой “программы по перемолке чисел” и такое замедление существенно.

Чтобы совместить скорость компилируемого языка и удобство python многие библиотеки поставляются вместе со скомпилированными модулями, написанными на C/++ (или другом компилируемом языке), а в python “прокидывают” интерфейс для взаимодействия с ними.

Установка NumPy

В anaconda numpy установлен по умолчанию, а установить его с помощью PyPI можно следующим образом:

python -m pip install numpy

Установив NumPy, чтобы начать им пользоваться, необходимо его импортировать.

import numpy as np

Библиотека NumPy используется настолько часто и настолько многими, что сложилась традиция импортировать NumPy с псевдонимом np. Любой программист, увидев где-то в коде выражение вида np.some_method() догадается, что вызывается метод some_method из библиотеки numpy и ему не потребуется искать глазами определение объекта np, чтобы понять, что скрывается за этим именем.

О массивах NumPy. Тип данных, размерность, форма.

Все элемента массива обязательно одного и того же типа. Этот тип можно узнать по полю dtype (data type). Этих типов может быть много, но большинство из них — стандартные числовые типы C/C++: np.bool8, np.int8, np.int16, np.int32, np.int64, np.unit8, np.unit16, np.unit32, np.uint64, np.float16, np.float32, np.float64, np.complex64, np.complex128 (подробнее про типы).

Note

Целые числа в массивах NumPy введут себя совсем не как тип int из python. Они всегда занимают определенное количество байт и склонны к переполнению, как в C/C++.

Так же в этих массивах можно хранить и другие типы данных, но тогда храниться в массиве будут указатели на них, а не сами объекты и большинство преимуществ массивов NumPy спадут на нет.

Кроме типа данных dtype у массива можно спросить его размерность ndim и его форму shape — длину массива вдоль каждого измерения. Эти измерения называются осями (axis в ед. числе и axes в мн. числе). Общее количество элементов в массиве (произведение количеств элементов вдоль каждой из осей) хранится в атрибуте size.

Все массивы должны быть “прямоугольными”, т.е. не может быть матрицы со строками разных длин.

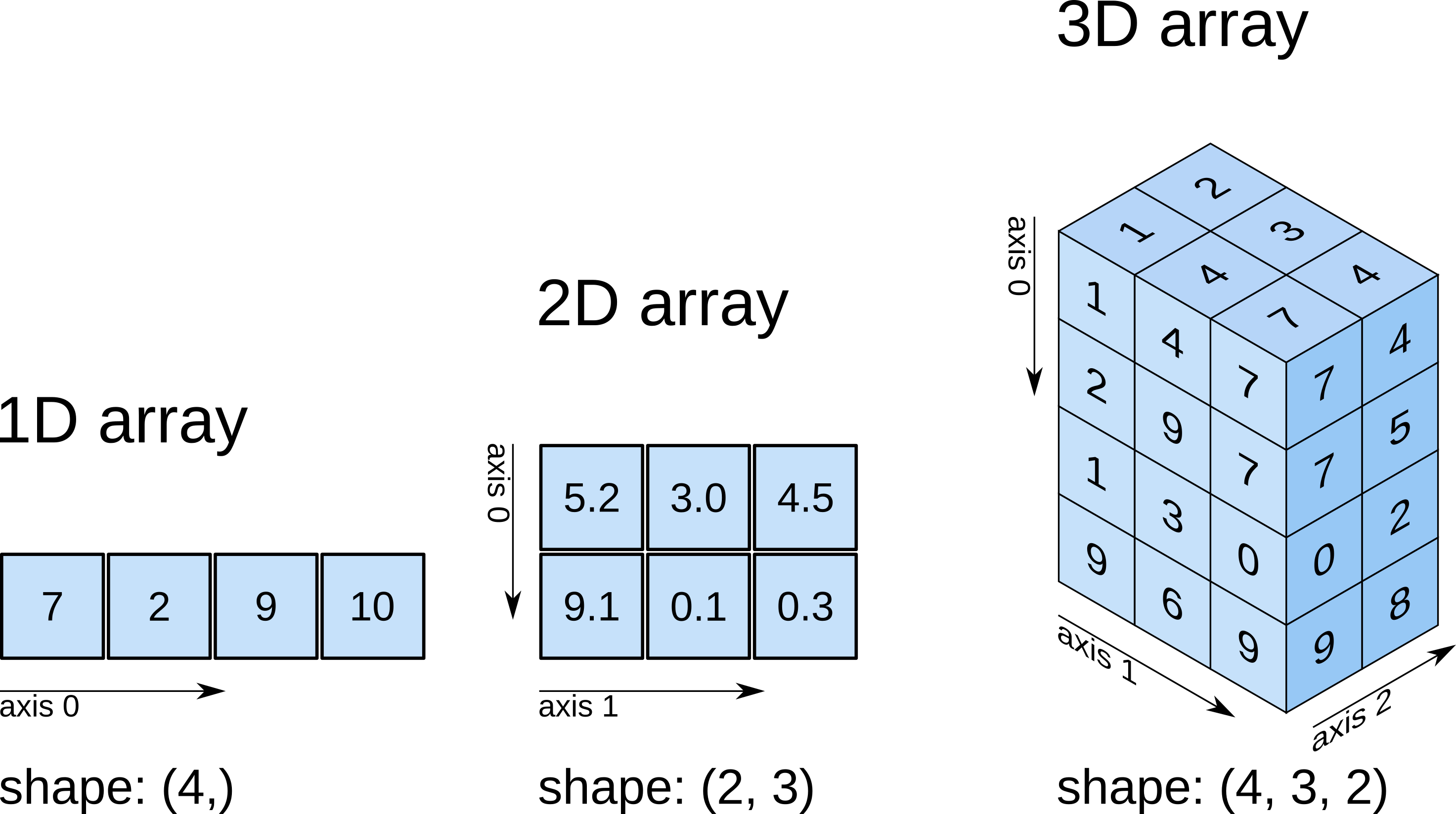
image

Создание массивов

Создавать массивы NumPy (ndarray) можно огромным количеством образом. Например, из списков (или любых других последовательностей) python. При этом итоговый тип данных в массиве определяется как самый общий, среди присутствующих в списке, если не указан явно.

# вектор (одномерный массив) из np.float64
a1D = np.array([1., 2, 3, 4]) 
print(repr(a1D), a1D.dtype, a1D.ndim, a1D.shape, sep="\n")

array([1., 2., 3., 4.])
float64
1
(4,)

# матрица (двухмерный массив) из целых чисел
a2D = np.array([[1, 2], [3, 4]]) 
print(repr(a2D), a2D.dtype, a2D.ndim, a2D.shape, sep="\n")

array([[1, 2],
       [3, 4]])
int32
2
(2, 2)

# Явно указан тип, тензор третьего ранга (трехмерный массив)
a3D = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]], dtype=np.float32) 
print(repr(a3D), a3D.dtype, a3D.ndim, a3D.shape, sep="\n")

array([[[1., 2.],
        [3., 4.]],

       [[5., 6.],
        [7., 8.]]], dtype=float32)
float32
3
(2, 2, 2)

Так же есть ряд встроенных функций, создающих массивы (array creation). Каждая из них принимает в качестве опционального аргумента dtype.

Метод

Аргументы

Описание

np.arange

start, stop, end

Аналог np.array(range), но можно использовать float в качестве аргументов

np.linspace

start, stop, num, endpoint=True

Разбиение отрезка [start, stop] на num отрезков, если передать в качестве endpoint=False, то последняя точка не включается

np.zeros

shape

Массив заданной формы из нулей

np.ones

shape

Массив заданной формы из единиц

np.random

Не метод, а подмодуль, содержащий методы создания массивов случайных значений

np.eye

n, m

Если m не указан, то квадратная единичная матрица размера nxn, иначе нулевая матрица размера nxm с единицами на диагонали

np.diag

v, k=0

Матрица с вектором v на главной диагонали (k=0) или на k-й диагонали

np.vand

x, N=None, increasing=False

Матрица Вандермонда из вектора x

Кроме того, существует ряд методов, позволяющих создавать массивы из других массивов.

Метод

Описание

np.hstack

Присоединение массивов вдоль строк

np.vstack

Присоединение массивов вдоль столбцов

np.dstack

Присоединение массивов “в глубину”

np.block

Составление массива из блоков

 
A = np.ones((2, 2))
B = 2 * A
C = 3 * A
D = 4 * A

print(np.block([[A, B], [C, D]]))

[[1. 1. 2. 2.]
 [1. 1. 2. 2.]
 [3. 3. 4. 4.]
 [3. 3. 4. 4.]]

Арифметические операции над массивами NumPy

Все основные арифметические операторы (+, -, *, /, //, %, **) перегружены для работы с массивами. Определим скаляры и векторы, чтобы разобраться, какие действия они позволяют выполнять.

x = np.array([0, 1, 2])
y = np.array([7, 13, 42])
alpha = np.pi 
beta = 3

A = np.eye(3)
B = np.ones((3, 3))

Если в арифметическом выражении участвуют скаляр и массив, то результатом является массив значений поэлементного применения указанной арифметической операции с скаляром. Т.е., можно, например, умножить массив на число или даже сложить массив с числом.

print(alpha * x)
print(alpha + x)
print(alpha - x)
print(alpha / y)
print(y / alpha)
print(y // beta)
print(y % beta)
print(x ** beta)

[0.         3.14159265 6.28318531]
[3.14159265 4.14159265 5.14159265]
[3.14159265 2.14159265 1.14159265]
[0.44879895 0.24166097 0.07479983]
[ 2.2281692   4.13802852 13.36901522]
[ 2  4 14]
[1 1 0]
[0 1 8]

Если в выражении участвует два массива, то они должны быть одинаковой формы, а арифметическая операция применяется поэлементно.

Note

Важно запомнить, что все арифметические операторы выполняют поэлементное преобразование. Это в каком-то смысле является стандартным поведением python и многие другие действия NumPy выполняет поэлементно. Далее рассматривается матричное умножение — принципиально не поэлементная операция.

print(x + y)
print(y - x)
print(x * y)
print(x / y)
print(x // y)
print(x % y)
print(x ** y)

[ 7 14 44]
[ 7 12 40]
[ 0 13 84]
[0.         0.07692308 0.04761905]
[0 0 0]
[0 1 2]
[0 1 0]

Матричное умножение

Оператор * совершает поэлементное умножение, в том числе и для для двухмерных массивов. Если хочется вложить в двухмерные массив смысл матрицы из линейной алгебры и умножить их как матрицы, то есть два пути:

a) Использовать оператор @:

print(A, B, A * B, A @ B, sep="\n" + "-" * 10 + "\n")

[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]
----------
[[1. 1. 1.]
 [1. 1. 1.]
 [1. 1. 1.]]
----------
[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]
----------
[[1. 1. 1.]
 [1. 1. 1.]
 [1. 1. 1.]]

b) Воспользоваться специальным типом np.matrix предназначенным для хранения именно двухмерных матриц.

A_matrix = np.matrix(A)
B_matrix = np.matrix(B)
print(repr(A_matrix), repr(B_matrix), repr(A_matrix * B_matrix), sep="\n" + "-" * 20 + "\n")

matrix([[1., 0., 0.],
        [0., 1., 0.],
        [0., 0., 1.]])
--------------------
matrix([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]])
--------------------
matrix([[1., 1., 1.],
        [1., 1., 1.],
        [1., 1., 1.]])

np.matrix наследуется от ndarray и отличается от него в следующем:

  • np.matrix обязательно двухмерный массив, а ndarray имеет произвольную размерность;

  • * имеет смысл поэлементного управления для ndarray и матричного умножения для np.matrix;

  • ** — поэлементное возведение в степень для ndarray и матричное возведение для np.matrix;

  • np.matrix.H и np.matrix.I возвращают сопряженную и обратную матрицу;

Warning

Создатели NumPy рекомендуют использовать ndarray, и не дают гарантию, что в одном из будущих обновлений np.matrix не пропадут из библиотеки.

Индексация

Индексация одномерных массивов ndarray осуществляется очень похоже на индексацию последовательностей python (списков, например).

print(a1D)
print(a1D[0], a1D[-1])

[1. 2. 3. 4.]
1.0 4.0

Индексация многомерных осуществляется несколько с новым синтаксисом.

print(a2D, end="\n" + "-"*10 + "\n")
print(a2D[0], end="\n" + "-"*10 + "\n")
print(a2D[-1, -1], a2D[-1][-1])

[[1 2]
 [3 4]]
----------
[1 2]
----------
4 4

print(a3D, end="\n" + "-"*10 + "\n")
print(a3D[0], end="\n" + "-"*10 + "\n")
print(a3D[-1, -1], a3D[-1][-1], end="\n" + "-"*10 + "\n")
print(a3D[-1, -1, -1])

[[[1. 2.]
  [3. 4.]]

 [[5. 6.]
  [7. 8.]]]
----------
[[1. 2.]
 [3. 4.]]
----------
[7. 8.] [7. 8.]
----------
8.0

Изменение формы массива

Можно изменять размерность и форму массива, но с условием, что общее количество элементов остается (size) неизменным.

  • np.reshape возвращает новый объект с измененной формой.

  • numpy.ndarray.resize изменяет сам объект.

  • numpy.ravel возвращает новый одномерный массив с теми же данными.

A = np.arange(24)
print(A)

[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]

B = A.reshape(4, 6)
print(B)

[[ 0  1  2  3  4  5]
 [ 6  7  8  9 10 11]
 [12 13 14 15 16 17]
 [18 19 20 21 22 23]]

C = A.reshape(4, 3, 2)
print(C)

[[[ 0  1]
  [ 2  3]
  [ 4  5]]

 [[ 6  7]
  [ 8  9]
  [10 11]]

 [[12 13]
  [14 15]
  [16 17]]

 [[18 19]
  [20 21]
  [22 23]]]

A.resize(2, 12)
print(A)

[[ 0  1  2  3  4  5  6  7  8  9 10 11]
 [12 13 14 15 16 17 18 19 20 21 22 23]]

A = np.ravel(A) # или A = A.ravel()
print(A)

[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23]

View. Разделяемое владение данными и копирование

На самом деле массивы ndarray устроены чуть сложнее. Массивы ndarray могут разделять одни и те же данные между собой. Массивы можно разделить на два вида: base и view. view — ndarray, который не имеет собственных данных, а ссылается на данные внутри массива base. base массив владеет данными, view лишь позволяет по-другому на них посмотреть.

Каждый ndarray представляет собой объект, который хранит не только указатель на данные (нечто очень похожее на C массив), но еще и метаданные, говорящие массиву, каким образом интерпретировать эти данные.

Рассмотрим пример. Создадим массив A и убедимся, что он владеет своими данными.

A = np.arange(6)
print(A)
print("Флаги массива A: \n", A.flags)

[0 1 2 3 4 5]
Флаги массива A: 
   C_CONTIGUOUS : True
  F_CONTIGUOUS : True
  OWNDATA : True
  WRITEABLE : True
  ALIGNED : True
  WRITEBACKIFCOPY : False
  UPDATEIFCOPY : False

Мы создали массив (ndarray) размера 6, который владеет данными [0, 1, 2, 3, 4, 5] типа np.int. Созданный массив мы связали с именем A. image Теперь создадим новый массив B путем изменения формы массива A методом reshape. Убедимся, что он использует те же данные.

B = A.reshape(2, 3)
print(B)
print("Массив B пользуется данными массива A?", B.base is A)
print("Флаги массива B: \n", B.flags)

[[0 1 2]
 [3 4 5]]
Массив B пользуется данными массива A? True
Флаги массива B: 
   C_CONTIGUOUS : True
  F_CONTIGUOUS : False
  OWNDATA : False
  WRITEABLE : True
  ALIGNED : True
  WRITEBACKIFCOPY : False
  UPDATEIFCOPY : False

Итак, массив содержит те же числа, но расположенные уже по строкам матрицы размера \(2 \times 3\). Напротив флага "OWNSDATA" стоит False, т.е. данными он не владеет. Картинка ниже объясняет, что произошло. Создался новый объект с новыми метаданными, который ссылается на тот же массив с данными. Эти новые метаданные указывают, что массив данных следует интерпретировать так, как будто в нём хранится матрица размера \(2 \times 3\), записанная по строкам друг за другом.

image

Создадим транспонированную матрицу методом transpose и убедимся, что она тоже использует данные исходного массива A.

C = B.transpose()
print(C)
print("Массив C пользуется данными массива A?", C.base is A)

[[0 3]
 [1 4]
 [2 5]]
Массив C пользуется данными массива A? True

Матрица C — транспонирование матрицы B. Под неё тоже не выделился новый массив с данными, а только лишь новые метаданные. В данном случае, метаданные указывают, что в массиве хранится матрица размера \(3 \times 2\), которая расположена в памяти таким образом, что первый индекс меняется быстрее второго (т.е. как бы по столбцам).

image

Продемонстрируем, что изменение элементов любого из этих массивов повлияет на остальные.

C[2, 1] = 42
print(A, B, C, sep="\n" + "-"*15 + "\n")

[ 0  1  2  3  4 42]
---------------
[[ 0  1  2]
 [ 3  4 42]]
---------------
[[ 0  3]
 [ 1  4]
 [ 2 42]]

previous

Сторонние библиотеки и пакетные менеджеры

next

Векторизация